Data-enabled Gradient Flow as Feedback Controller - Regulation of Linear Dynamical Systems to Minimizers of Unknown Functions

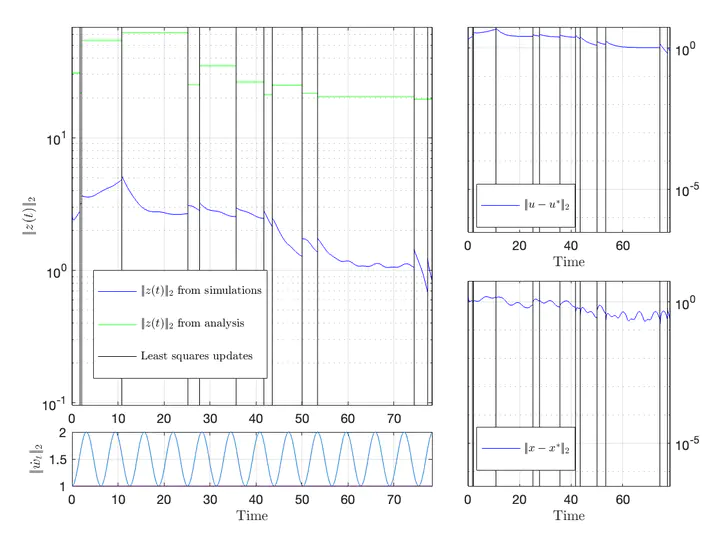
This paper considers the problem of regulating a linear dynamical system to the solution of a convex optimization problem with an unknown or partially-known cost. We design a data-driven feedback controller - based on gradient flow dynamics - that (i) is augmented with learning methods to estimate the cost function based on infrequent (and possibly noisy) functional evaluations; and, concurrently, (ii) is designed to drive the inputs and outputs of the dynamical system to the optimizer of the problem. We derive sufficient conditions on the learning error and the controller gain to ensure that the error between the optimizer of the problem and the state of the closed-loop system is ultimately bounded; the error bound accounts for the functional estimation errors and the temporal variability of the unknown disturbance affecting the linear dynamical system. Our results directly lead to exponential input-to-state stability of the closed-loop system. The proposed method and the theoretical bounds are validated numerically. This paper was accepted for publication to the 4th Annual Learning for Dynamics and Control Conference, 2022.