Online Optimization of Dynamical Systems with Deep Learning Perception

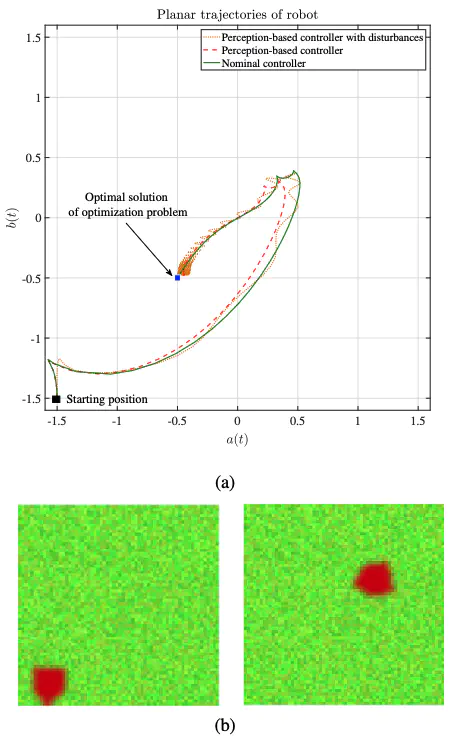
This paper considers the problem of controlling a dynamical system when the state cannot be directly measured and the control performance metrics are unknown or partially known. In particular, we focus on the design of data-driven controllers to regulate a dynamical system to the solution of a constrained convex optimization problem where i) the state must be estimated from nonlinear and possibly high-dimensional data; and, ii) the cost of the optimization problem – which models control objectives associated with inputs and states of the system – is not available and must be learned from data. We propose a data-driven feedback controller that is based on adaptations of a projected gradient-flow method; the controller includes neural networks as integral components for the estimation of the unknown functions. Leveraging stability theory for perturbed systems, we derive sufficient conditions to guarantee exponential input-to-state stability (ISS) of the control loop. In particular, we show that the interconnected system is ISS with respect to the approximation errors of the neural network and unknown disturbances affecting the system. The transient bounds combine the universal approximation property of deep neural networks with the ISS characterization. Illustrative numerical results are presented in the context of control of robotics and epidemics. This paper was accepted for publication to the IEEE Open Journal of Control Systems - Special Section on Machine Learning with Control, 2022.