Online Optimization of Linear Time Invariant Dynamical Systems with Cost Perception
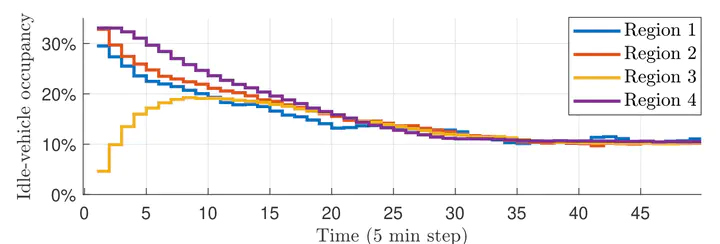 States of the ride-share scheduling problem using an estimated gradient obtained via a feedforward neural network.
States of the ride-share scheduling problem using an estimated gradient obtained via a feedforward neural network.This paper considers the problem of regulating a discrete-time linear time-invariant (LTI) system to solution trajectories of a convex optimization problem, with an unknown cost. We propose a data-driven, gradient-based feedback controller that uses estimates of the cost functions obtained by a trained neural network to control the LTI system. We identify sufficient conditions to guarantee exponential input-to-state stability (ISS) of the closed loop system with respect to errors due to disturbances, temporal variability of the cost functions, and the need to use estimated costs from a neural network. Finally, we provide an illustrative numerical example in the context of online ride-share scheduling.